Queueing Questions

[ACM SIGMETRICS Performance Evaluation Review]

【Title】The most common queueing theory questions asked by computer systems practitioners

本文探讨了业界实践者反复提出的五个性能问题：

我的系统利用率很低，为什么作业延迟却这么高？
我应该怎么做才能降低作业延迟？
如果我不知道哪些作业是短作业，怎样才能优先处理短作业？
如果有些作业比其他作业更重要，我该如何在重要性和大小之间进行权衡？
当处理的是闭环系统而不是开放系统时，答案会发生怎样的变化？
所有这些问题都可以通过排队论得到简单的解答。本文将对这些问题及其答案进行详细阐述。

Q1

【Q1】我的系统利用率很低，为什么作业延迟却这么高？

为什么系统利用率可能很低，但延迟却很高？为了让这个问题更具体一些，考虑图 1 所示的单服务器队列，其中作业按照先到先服务（FCFS）的顺序处理。这里，λ 表示作业到达的速率（个/秒）。作业具有不同的大小（服务需求），其中 S 是表示作业大小（以秒为单位）的随机变量。利用率（负载），记作 ρ，是服务器在长时间内处于忙碌状态的时间比例，其中 ρ = λ · E[S]。作业的响应时间 (T) 指的是从作业到达直到完成的时间。作业的延迟 (D)，也称为排队时间，就是 T − S，即作业响应时间减去作业大小。

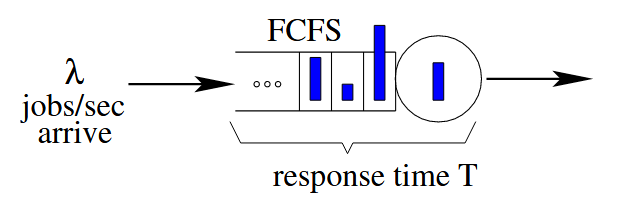
直观上看，如果服务器的利用率只有 ρ = 20%，那么平均作业延迟应该很低。然而，这种直觉是错误的！实际上，在单服务器队列的情况下，作业的平均延迟取决于三个因素：

(i) 利用率 ρ
(ii) 作业服务时间的变化性
(iii) 作业到达间隔时间的变化性。
Kingman 的近似公式 [20] 表示：
$E [D e l a y] \approx \frac{ρ}{1 - ρ} \cdot (\frac{C_{S}^{2} + C_{A}^{2}}{2}) \cdot E (S)$

$C^{2}_{S}$ $C_{S}^{2}=Var(S)/E(S)^{2}$ $C_{A}^{2}$ 是作业到达间隔时间的对应量。作业服务时间的变化性会导致较高的延迟，因为这意味着短作业最终会排在长作业之后，从而“继承”长作业的延迟。同样，到达间隔时间的变化性也是一个问题，因为这意味着作业会以突发的方式到达。

$C_{S}^{2}$ $C_{S}^{2}$ $C_{S}^{2}$ 值很容易掩盖低 ρ 的影响，从而导致即使在利用率较低的情况下，平均延迟依然很高。

说白了就是尽管服务器利用率很低，但短请求也有可能排在长请求后面，继承长请求的延迟。

Q2

【Q2】我应该怎么做才能降低作业延迟？

有三种主要的解决策略：

Scheduling to Favor Short Jobs
- 第一种解决方案是采用偏向短作业的调度策略。理想情况下，应始终按照最短剩余处理时间（SRPT）原则进行调度，即随时抢占式地运行即将最快完成的作业。虽然SRPT适用于任何作业到达流且具有最优性，但研究发现更简化的SRPT变体也能达到近乎相同的效果。例如，仅使用3个规模分桶进行SRPT调度即可获得相近的平均延迟[18, 21]。同理，采用抢占式最短作业优先（PSJF）策略也能实现近乎相当的性能。该策略还可扩展至k服务器场景——始终运行剩余处理时间最短的k个作业[11]。
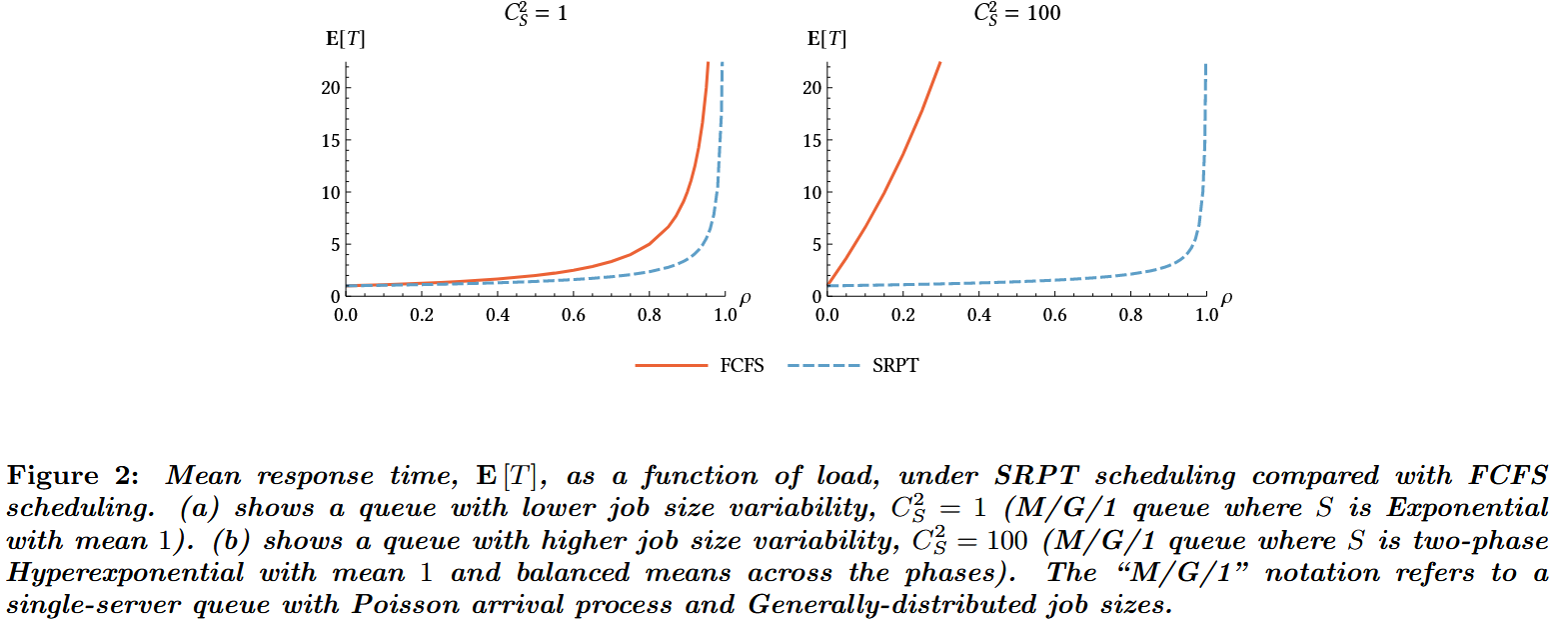
- 当作业服务需求的变异性较高时（如图2所示），SRPT调度相比先到先服务（FCFS）具有显著优势，因为它能确保短作业不会因长作业而长时间阻塞等待。然而实践者对于采用SRPT心存顾虑，他们担心长作业会遭受不公正的延迟惩罚。事实上，在系统利用率不过高的情况下（参见[5,30]），长作业并未受到相对于短作业的不公平对待；但这些担忧根深蒂固，导致SRPT调度的实际应用远低于理论预期。

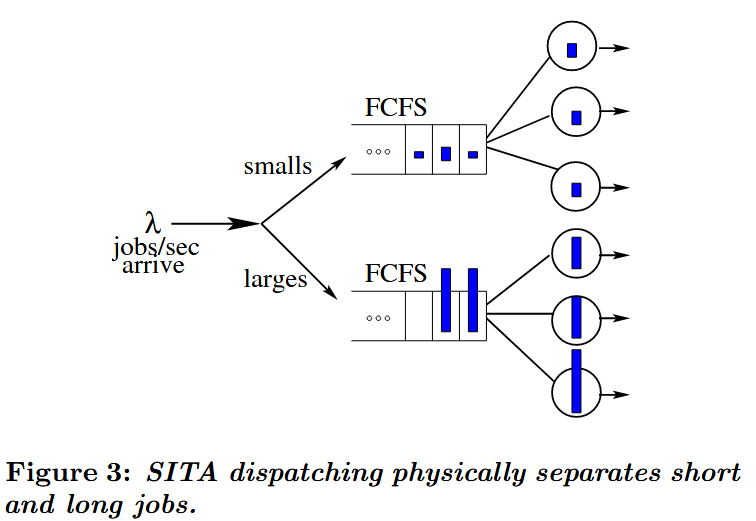
Dispatching to Isolate Short Jobs
- 另一种解决方案是将短作业与长作业进行物理隔离。例如，[7,15]中提出的规模区间任务分配（SITA）方案（如图3所示）将短作业调度至一组服务器，而将长作业分配至另一组服务器。
- SITA方案能显著降低平均延迟，因为短作业无需在长作业后排队等待。特别值得注意的是，短作业仅需面对其他短作业的规模变异性和负载压力。唯一的关键问题在于如何界定"短作业"与"长作业"的划分阈值。一种解决方案是采用SITA-E方法，通过设置阈值使长短作业系统的负载达到均衡。在典型计算工作负载中（规模最大的1%作业往往承载绝大部分负载），SITA-E会将不足1%的作业分配至长作业队列。还可根据作业规模分布特性进一步优化阈值设定，具体方法参见文献[19]。

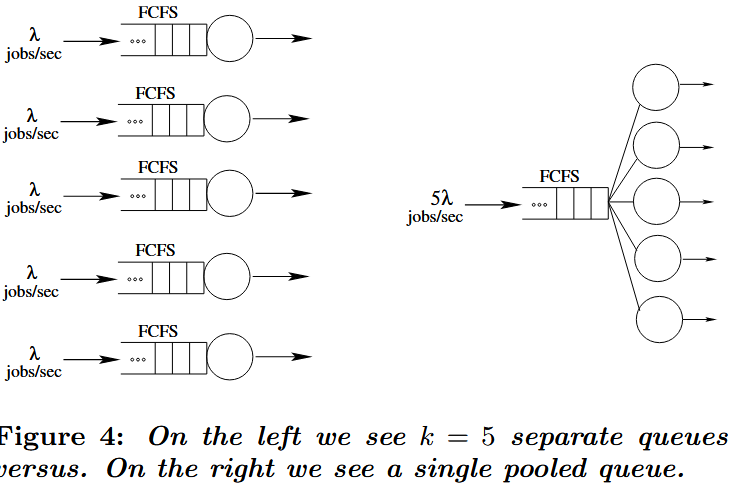
Pooling Resources
- $\lambda$ $E(S)$ $\rho = \lambda \cdot E(S)$ $k\lambda$ $k$ $\rho = \frac{k \lambda \cdot E(S)}{k}=\lambda \cdot E(S)$ ),与原始系统保持一致。但整合后系统的延迟显著低于原始系统。例如当作业规模服从指数分布时（参见[14, p.270]）：
  $E [D e l a y o f j o b s t h a t q u e u e i n p o o l e d s y s t e m] = \frac{1}{k λ} \cdot \frac{ρ}{1 - ρ}$
  关键在于：由于ρ和λ是常数，整合后系统的延迟会随k值增加呈倍数级下降。对于一般分布形式的作业规模，资源整合能带来更显著的效益提升（参见[22]）。

Q3

【Q3】如果我不知道哪些作业是短作业，怎样才能优先处理短作业？

在第一章节中，我们发现延迟主要与作业规模的高变异性密切相关。第二章则表明，使短作业与长作业实现一定程度的隔离能有效缓解高变异性的影响。这种隔离既可通过赋予短作业优先权实现（如2.1节所述），也可通过为短作业配置专属资源达成（如2.2节方案）。但若无法预先获知作业规模，我们应如何最小化延迟？我们将首先探讨替代调度策略，继而研究在作业规模未知情况下的分派策略。

相较于2.1节方案，存在诸多无需知晓作业规模却能有效应对变异性问题的调度替代方案。其中最简易的是处理器共享（PS）调度，该方案通过在队列中所有作业间分时共享服务器资源，使短作业无需因长作业而阻塞等待。但我们可以进一步利用作业的"年龄"（即已获得的服务量）作为剩余规模的代理指标：在具有递减失效率（DHR）特性的系统中，年龄较低的作业往往更可能快速完成，而年龄较高的作业通常剩余处理时间更长。此时按年龄排序并优先处理低年龄作业的策略具有显著优势[1]，相关算法称为最小已服务（LAS）调度（参见[13]）。

若作业规模分布不具DHR特性，则可结合年龄信息与分布规律，通过计算期望剩余处理时间进行排序。具体而言，若用随机变量S表示作业规模，a表示当前年龄，则期望剩余规模可计算为：

E [S - a | S > a]

继而采用始终（抢占式）运行最小期望剩余处理时间（SERPT）作业的调度策略。在作业规模未知的情况下，最优调度策略是吉廷斯指数策略(Gittins)——该策略通过综合评估作业的期望剩余规模与下一时刻完成概率对作业进行排序。虽然吉廷斯指数策略具有理论最优性[2,3,10,26]，但其实现相当复杂；实践中SERPT通常能达成相近效果。这些策略在M/G/1模型下的精确响应时间推导详见[28]。上述所有策略均可推广至k服务器场景（M/G/k模型），参见[11,24,25]。

图5（上图）展示了一个作业规模分布：作业规模范围0到16且具有不同分布密度。虽然单个作业的具体规模未知，但可通过作业年龄（即已获得的服务量）进行推断。如图5（下图）所示，作业的期望剩余规模随年龄动态变化：初始阶段期望剩余规模较小（因多数作业位于分布的第一"峰值"区）；当作业年龄越过第一个分布峰值后，期望剩余规模开始上升；越过第二个峰值时则会再次跃增。

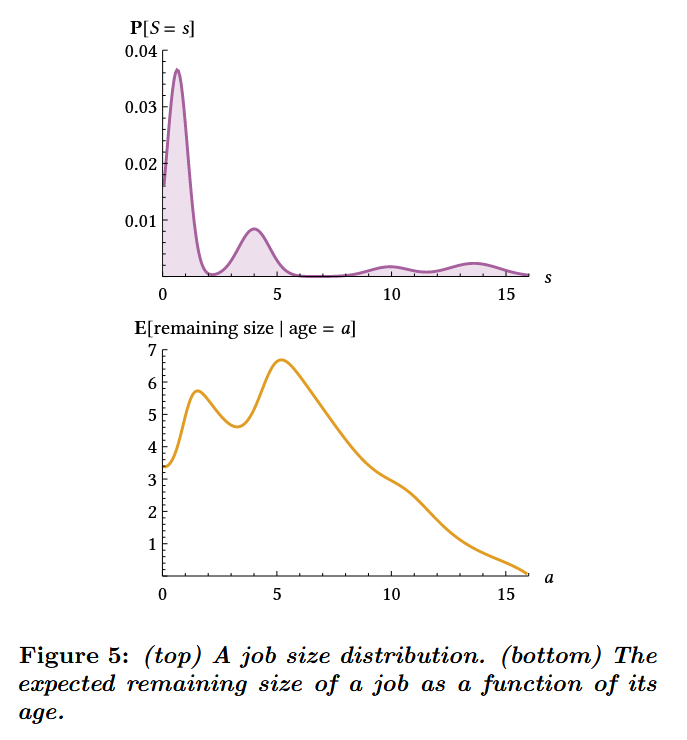
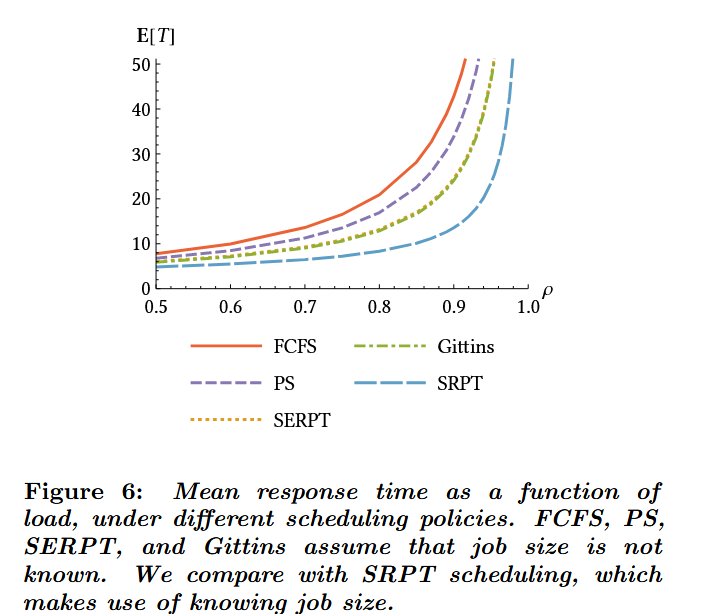
图6展示了当作业规模遵循图5分布时，不同调度策略（FCFS、PS、SERPT、吉廷斯和SRPT）下的平均响应时间。其中FCFS、PS、SERPT和吉廷斯策略均假设作业规模未知——SERPT和吉廷斯通过利用图5（下图）所示的期望剩余作业规模实现了优异性能。如图所示，SERPT策略的性能与最优的吉廷斯策略极为接近，更多讨论参见[27]。

除2.2节的SITA策略外，还存在无需知晓作业规模的分派替代方案。例如基于规模预测的任务分配（TAGS）策略[4,12]：该策略假设所有作业初始均为短作业，将其全部发送至短作业队列，但会对短作业队列中的所有作业设置运行时间上限；若作业未在"短作业上限"时间内完成，则将其重启并转移至长作业队列。通过这种方式，TAGS有效限制了长作业对短作业的性能影响。当然，2.3节所述的资源整合方案也是SITA的可行替代方案（同样无需知晓作业规模）。关于资源整合与基于SITA算法性能对比的讨论详见[16]和[17]。

Q4

【Q4】如果有些作业比其他作业更重要，我该如何在重要性和大小之间进行权衡？

HOW DO I NEGOTIATE IMPORTANCE VERSUS SIZE ?

若某些作业具有更高重要性（或更高价值），标准解决方案是建立优先级队列结构——让高重要性作业获得优先权并能抢占低优先级作业。但当最重要作业均具有较大剩余规模，而次要作业却拥有极小剩余规模时，我们是否仍能通过严格优先处理重要作业来实现最大价值收益？这个关于重要性与规模权衡的问题在排队论中已有深入研究。

我们引入作业的"持有成本"概念：该成本以美元/秒为计量单位，表示系统因未完成该作业而持续产生的损失率。换言之，持有成本即因延迟处理作业而持续消耗的资金速率。持有成本越高的作业通常具有更高的"价值"。

在时间点t的系统总持有成本为：

T o t a l H o l d i n g C o s t (t) = \sum_{j o b s j i n s y s t e m a t t i m e t}^{} (h o l d i n g c o s t o f j o b j)

我们的目标是最小化期望持有成本，即时间点t总持有成本的时间平均值：

E [H o l d i n g C o s t] = lim_{μ \to \infty} \frac{1}{μ} \int_{0}^{μ} T o t a l H o l d i n g C o s t (t) d t

最小化期望持有成本的算法被称为c-μ规则[6]，该规则通过为每个作业分配索引值实现优化：

I n d e x (j o b) = \frac{H o l d i n g c o s t o f j o b}{R e m a i n i n g s i z e o f j o b}

该规则将最高优先级分配给索引值最大的作业。通过这种方式，cμ规则会优先处理持有成本高或剩余规模小的作业。虽然cμ规则在最坏情况下并非最优，但在包括M/G/1队列在内的多种场景中具有最优性[26]。

Q5

【Q5】当处理的是闭环系统而不是开放系统时，答案会发生怎样的变化？

至此我们一直假设系统内的作业到达流是外生的（外部产生），即新作业到达不受系统内部状态影响。与之相反，某些系统遵循闭环到达模型：新作业的到达仅由作业完成事件触发（可能附带称为"思考时间"的延迟）。也就是说，只有当某个作业完成后（经过一段思考期），新作业才能进入系统。在这类闭环配置中，通常存在同时驻留系统作业数量的上限，称为多道程序水平（MPL）。

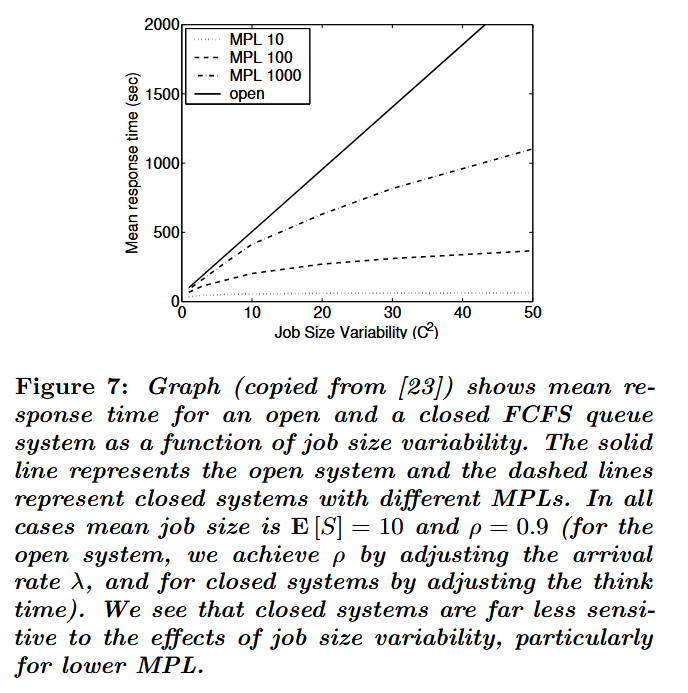
如文献[23]所述，闭环系统与开放系统的性能特征存在显著差异——即使两者在相同负载（利用率）ρ下运行。闭环系统的延迟通常明显更低：作业规模变异性对开放系统延迟有重大影响，但对闭环系统作业延迟的影响则弱得多（参见图7）。因此，虽然开放系统中必须通过偏向短作业（或潜在短作业）的调度策略来应对变异性，但基于作业规模的调度在闭环系统中重要性大幅降低。

直观而言，这种差异源于闭环系统的作业数量受限于MPL：即使MPL值较高（达数百量级），但仅存在数量上限这一事实就意味着闭环系统的平均延迟显著降低，高变异性影响也随之缓解——当作业总数较少时，短作业被长作业阻塞的现象自然减少。鉴于两类系统的本质差异，在开始任何性能讨论时，必须首先明确所处理的系统配置类型。同理，通过工作负载生成器测试系统时，也需清醒认知其采用的是闭环生成模式还是外生生成模式。

参考文献：

[1] Samuli Aalto and Urtzi Ayesta. Optimal scheduling of jobs with a DHR tail in the M/G/1 queue. In VALUETOOLS 2008, October 2008.

[2] Samuli Aalto, Urtzi Ayesta, and Rhonda Righter. On the Gittins index in the M/G/1 queue. Queueing Systems, 63(1):437–458, 2009.

[3] Samuli Aalto, Urtzi Ayesta, and Rhonda Righter. Properties of the Gittins index with application to optimal scheduling. Probability in the Engineering and Informational Sciences, 25(3):269–288, 2011.

[4] Eitan Bachmat, Josu Doncel, and Hagit Sarfati. Analysis of the task assignment based on guessing size policy. Performance Evaluation, 142, 2020.

[5] Nikhil Bansal and Mor Harchol-Balter. Analysis of SRPT scheduling: Investigating unfairness. In Proceedings of ACM SIGMETRICS, pages 279–290, Cambridge, MA, June 2001.

[6] D.R. Cox and W.L. Smith. Queues. Kluwer Academic Publishers, 1971.

[7] Mark Crovella, Mor Harchol-Balter, and Cristina Murta. Task assignment in a distributed system: Improving performance by unbalancing load. In Proceedings of the ACM SIGMETRICS Joint International Conference on Measurement and Modeling of Computer Systems, pages 268–269, June 1998. Poster Session.

[8] Anshul Gandhi, Sherwin Doroudi, Mor Harchol-Balter, and Alan Scheller-Wolf. Exact analysis of the M/M/k/setup class of Markov chains via Recursive Renewal Reward. In ACM SIGMETRICS 2013 Conference on Measurement and Modeling of Computer Systems, pages 153–166, 2013.

[9] Anshul Gandhi and Mor Harchol-Balter. How data center size impacts the effectiveness of dynamic power management. In 49th Annual Allerton Conference on Communication, Control, and Computing, pages 1164–1169, Urbana-Champaign, IL, September 2011.

[10] John C. Gittins, Kevin D. Glazebrook, and Richard Weber. Multi-armed Bandit Allocation Indices. John Wiley & Sons, 2011.

[11] Isaac Grosof, Ziv Scully, and Mor Harchol-Balter. SRPT for multiserver systems. Performance Evaluation, 127:154–175, November 2018.

[12] Mor Harchol-Balter. Task assignment with unknown duration. Journal of the ACM, 49(2):260–288, March 2002.

[13] Mor Harchol-Balter. Queueing disciplines. Wiley Encyclopedia of Operations Research and Management Science, 2011.

[14] Mor Harchol-Balter. Performance Modeling and Design of Computer Systems: Queueing Theory in Action. Cambridge University Press, 2013.

[15] Mor Harchol-Balter, Mark Crovella, and Cristina Murta. On choosing a task assignment policy for a distributed server system. In Lecture Notes in Computer Science, No. 1469: 10th International Conference on Modeling Techniques and Tools for Computer Performance Evaluation, pages 231–242, September 1998.

[16] Mor Harchol-Balter, Alan Scheller-Wolf, and Andrew Young. Surprising results on task assignment in server farms with high-variability workloads. In ACM SIGMETRICS 2009 Conference on Measurement and Modeling of Computer Systems, pages 287–0298, 2009.

[17] Mor Harchol-Balter, Alan Scheller-Wolf, and Andrew Young. Why segregating short jobs from long jobs under high variability is not always a win. In Forty-seventh Annual Allerton Conference on Communication, Control, and Computing, pages 121–127, University of Illinois at Urbana-Champaign, October 2009.

[18] Mor Harchol-Balter, Bianca Schroeder, Nikhil Bansal, and Mukesh Agrawal. Size-based scheduling to improve web performance. ACM Transactions on Computer Systems, 21(2):207–233, May 2003.

[19] Mor Harchol-Balter and Rein Vesilo. To balance or unbalance load in size-interval task allocation. Probability in the Engineering and Informational Sciences, 24:219–244, 2010.

[20] J.F.C. Kingman. Two similar queues in parallel. Biometrika, 48:1316–1323, 1961.

[21] Behnam Montazeri, Yilong Li, Mohammad Alizadeh, and John K. Ousterhout. Homa: A receiver-driven low-latency transport protocol using network priorities. In Proceedings of SIGCOMM 2018, pages 221–235. ACM SIGCOMM, 2018.

[22] Alan Scheller-Wolf and Rein Vesilo. Structural interpretation and derivation of necessary and sufficient conditions for delay moments in fifo multiserver queues. Queueing Systems, 54(3):221–232, 2006.

[23] Bianca Schroeder, Adam Wierman, and Mor Harchol-Balter. Open versus closed: a cautionary tale. In Proceedings of Networked Systems Design and Implementation (NSDI), 2006.

[24] Ziv Scully, Isaac Grosof, and Mor Harchol-Balter. The Gittins policy is nearly optimal in the M/G/k under extremely general conditions. Proceedings of ACM on Measurement and Analysis of Computer Systems (POMACS/SIGMETRICS), 4(3):1–29, 2020. Article 43.

[25] Ziv Scully, Isaac Grosof, and Mor Harchol-Balter. Optimal multiserver scheduling with unknown job sizes in heavy traffic. In 38th International Symposium on Computer Performance, Modeling, Measurement, and Evaluation (IFIP PERFORMANCE 2020), Milan, Italy, November 2020.

[26] Ziv Scully and Mor Harchol-Balter. The Gittins policy in the M/G/1 queue. In 19th International Symposium on Modeling and Optimization in Mobile, Ad hoc, and Wireless Networks (WiOpt ’21), Philadelphia, PA, October 2021.

[27] Ziv Scully and Mor Harchol-Balter. How to schedule near-optimally under real-world constraints. arXiv, 2021.

[28] Ziv Scully, Mor Harchol-Balter, and Alan Scheller-Wolf. SOAP: One clean analysis of all age-based scheduling policies. Proceedings of ACM on Measurement and Analysis of Computer Systems (POMACS/SIGMETRICS), 2(1):1–30, 2018. Article 16.

[29] Muhammad Tirmazi, Adam Barker, Nan Deng, MD E. Haque, Zhijing Gene Qin, Steven Hand, Mor Harchol-Balter, and John Wilkes. Borg: The next generation. In Proceedings of the Fifteenth European Conference on Computer Systems (EuroSys ’20), pages 1–14, Greece, April 2020.

[30] Adam Wierman and Mor Harchol-Balter. Classifying scheduling policies with respect to unfairness in an M/GI/1. In Proceedings of ACM SIGMETRICS, pages 238–249, San Diego, CA, June 2003.

M/M/1 & M/M/K模型

内存系统研究课题探索

SOSP'24 Colloid把排队论Little's Law带入分层内存系统，通过平衡延迟以达到（最优）吞吐量。

Little's Law适合评估稳态系统的排队延迟，但任务处理的时间不只是包含请求的排队，以及系统可能并非出于稳态，且可能面对多个等效服务器。所以其实能够继续探索的空间还有很多：

【Topic#1】面向云服务场景的低尾延迟分层内存系统

传统的分层内存系统更关注于降低平均访问延迟或者试图达到最佳吞吐量，然而新兴云服务等应用需要保障用户体验，提升SLO，因此对于此类应用，降低尾延迟对于用户体验至关重要。
QoS-Aware的分层内存系统也可以做，但已经有人做了，而且容易A+B的增量创新（hard to be accepted）

【Topic#2】面向云服务的VM性能优化

感兴趣，可以直接邮件联系我 lujhcoconut@foxmail.com