MLSys / LLMSys
机器学习系统能从示例中学习,通过自我改进产生准确的结果,而无需程序员明确编码。机器学习的目标:通过数据学习进行预测。
MLSys在现在的工作中非常火热,如之前OSDI ASPLOS写的Memstrata以及Pond等文章,最后都是基于机器学习搞一个模型。又包括FAST的GLCache,ISCA的Sibyl也都是通过强化学习的方式去优化cacheline在cache的放置策略或者是page在heterogeneous memory中不同tier之间的数据放置和迁移策略。又比如ATC的Calchas对HBM故障做预测也是采用随机森林的方法。
做系统体系结构相关的研究工作的时候,很难能够想到一些特别巧妙的方法,但还想基于一些发现做优化的时候,ML就是一个很好的工具。虽然顶会上利用ML的方式可能已经让人审美疲劳,但是ML用在一些非常amazing的motivation上也能出一个很好的工作。总之就是,现在做sys/arch几乎对这个已经是不会不行的状态。
机器学习的参考资料已经足够多了,这里就无需赘述太多,尤其是涉及数学证明与推导的部分。
LLM这么火,也想沾点边。LLM这块目前这个部分暂时以应用开发为主。后续会独立出单独的章节丢在主页上。
Machine Learning
快速入门
主要的三个分类是:回归、分类和结构化学习
举个回归的例子,假设机器要预测未来某一个时间的 PM2.5 的数值。机器要找一个函数 f,其输入是可能是种种跟预测 PM2.5 有关的指数,包括今天的 PM2.5 的数值、平均温度、平均的臭氧浓度等等,输出是明天中午的 PM2.5的数值,找这个函数的任务称为回归(regression)。
分类任务要让机器做选择题。人类先准备好一些选项,这些选项称为类别(class),现在要找的函数的输出就是从设定好的选项里面选择一个当作输出,该任务称为分类。举个例子,每个人都有邮箱账户,邮箱账户里面有一个函数,该函数可以检测一封邮件是否为垃圾邮件。分类不一定只有两个选项,也可以有多个选项。AlphaGo 也是一个分类的问题。
机器不只是要做选择题或输出一个数字,而是产生一个有结构的物体,比如让机器画一张图,写一篇文章。这种叫机器产生有结构的东西的问题称为结构化学习。
模型(model)的概念:带有未知参数的函数
特征(feature)的概念:函数里已知的来自于后台的信息
权重与偏置(weight and bias): 如y=ax+b ,a就是权重、b就是偏置
损失(loss)函数:损失也是一个函数,输入是模型里的参数,例如上一个例子,损失函数可以标记为L(a,b)。这个函数值就代表了这一组参数是好还是不好。至于损失函数如何定义,方法还是比较多的。
误差表面:说白了就是可以理解为是损失函数(实验了不同参数,得到了不同的损失)的等高线(维度不限)图。
解最优化问题:说白了就是找损失最小的位置。但有的时候不必要求解最优,次优较优的解都可算可行解。追寻最优解的代价是不确定的。因此一种常见的优化方法是梯度下降。梯度下降说白了就是找当前所在位置局部区域的极小值,所以这玩意儿基本得不到最优解,甚至不一定有解(导数都没有怎么求导?)。
梯度下降还会涉及到每次下降多少的问题:1)一个是当前位置的斜率,没啥好解释的。2)另一个就是学习率这种人工指定的超参数。学习率越大,那每次下降的就多一点,学的就会快一点。还有像手动设置更新次数这种也是超参数。
深度学习框架(例如PyTorch)中,会帮你自动算微分,就比较简单。
像y=ax+b这种线性模型,怎么画都是一条直线,很显然生活里哪有这么多场景是能够直接直线就能近似。再怎么简化抽象,我不想近似出平滑的曲线,也得有个折线吧。这就是分段线性曲线。
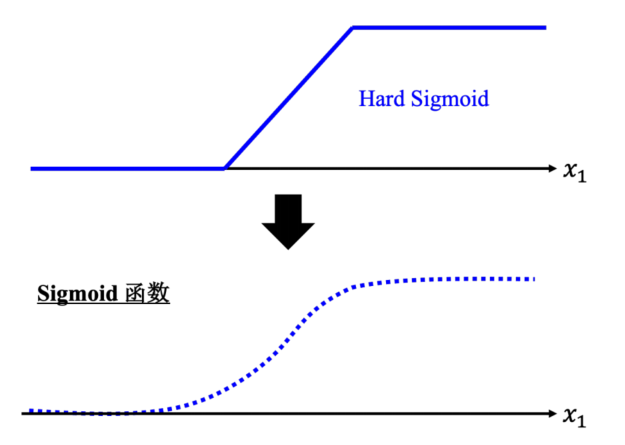
一种经典的写法就是利用Hard Sigmoid函数,给定一组Hard Sigmoid函数和常数,只要给的足够多,就拥有了整个世界。但写一组Hard Sigmoid函数一看就不容易,优化是用曲线去逼近直线(没错,就是用曲线逼近直线)的sigmoid函数。只要调一下sigmoid函数的参数,然后叠起来就能得到分段线性函数。
于是你很快发现,sigmoid叠多少个也是你决定的,所以Sigmoid叠加数量也显然是一个超参数。

叠的多了,自然就灵活多了。原来的损失函数L(a,b)就一对a,b不知道,现在叠了这么多,相当于叠了一个就多一组未知参数。那很显然向量化这个问题就可以了。让一组数据得到损失就行。
初始解为θ<0>,为了梯度下降,就对代入初始解的损失函数微分得到新的向量g,就是L对θ求的偏导的向量。
初始解向量减去学习率与g向量的积就得到了一组新的向量,也就是更新了一轮参数。以此类推知道梯度为0或者人为(超参数)中止他。
梯度下降的细节
批量(batch)处理:本来是所有数据拿来算损失,现在是选1个batch拿来算一个loss,再用这个loss算一个梯度,再用这个梯度更新一下参数。所以所谓的一次回合(epoch),就是所有的batch都拿来算了一遍。
除了Sigmoid之外,还有一个著名常用的激活函数:ReLU,就是一个横折的结构。

Sigmoid ReLU这种激活函数也被称作神经元,很多神经元就构成了神经网络,一排就是一层,这就是所谓的隐藏层,隐藏层多了就可以理解为深了,这就是深度学习。
在训练数据和测试数据上的结果是不一致的,这种情况称为过拟合(overfitting)。
深度学习的训练会用到反向传播(BackPropagation,BP),其实它就是比较有效率、算梯度的方法
机器学习框架
首先是需要有训练数据和测试数据,然后就是训练:
写一个有未知数θ的函数,θ代表一个模型里所有未知参数fθ(x) 的意思就是函数叫 fθ(x),输入的特征为 x
定义损失,就是一个接受输入参数判断好坏的函数
解最优化问题